- Það er samfellt á lokaða bilinu [a, b]
- Það er samfellt diffranlegt á opna bilinu ]a, b[
- Gildi þess í a og b eru þau sömu, það er f(a) = f(b)
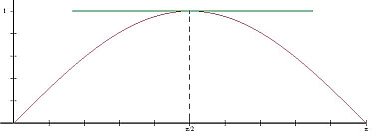
Fyrir gefið bil er til fullt af föllum sem uppfylla fyrstu tvö skilyrðin í reglu Rolle, en taka ekki sama gildið í endapunktum þess. Við erum náttúrlega ósátt með að geta ekki notað regluna okkar á þessi föll, en ef f er slíkt fall þá getum við spurt okkur hvort til sé einhver fasti r þannig að fallið \[g(x):=f(x)+r(x)\] taki sömu gildi í endapunktum bilsins, svo við getum beitt reglu Rolles á fallið g. Með því að athuga gildi g í endapunktum bilsins og nota smá algebru er einfalt að sjá að slíkt r er til, og þegar við beitum reglu Rolle á þetta nýja fall fæst meðalgildissetningin. Hún segir að ef fall f sem er skilgreint á bili [a, b] fullnægir tveimur fyrstu skilyrðunum í reglu Rolles, þá er til punktur c á bilinu þannig að gildi f '(c) sé jafnt hallatölu línunnar í gegnum endapunkta fallsins. Með öðrum orðum gildir í punktinum c að: \[f'(c)=\frac{f(b)-f(a)}{b-a}\] Eflaust er best að skilja þessa reglu ef við tökum hraða bíls sem dæmi. Ímyndum okkur bíl sem er á ferð með hraðanum 100 km/klst og hægir á sér þar til hann stöðvast, þannig að meðalhraði bílsins frá því við byrjuðum að fylgjast með honum og þar til hann stöðvaðist hafi verið 50 km/klst. Þar sem bíllinn var upphaflega á hraðanum 100 km/klst og kláraði ferðalagið í kyrrstöðu, þá liggur fyrir að á einhverju augnabliki var hraði hans nákvæmlega 50 km/klst, eða jafn mikill og meðalhraðinn, en það er einmitt það sem setningin segir okkur. Þetta dæmi má setja fram myndrænt með grafi sem sýnir hvernig færsla bílsins breytist með tíma:
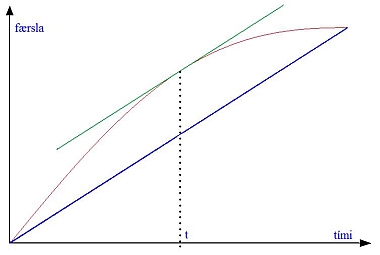
Fjólublái ferillinn á myndinni táknar færslu bílsins, og bláa línan liggur á milli upphafs- og endapunkta ferilsins, en hallatala hennar er jöfn meðalhraða bílsins. Ef við tökum snertil við ferilinn, þá svarar hallatala hans til hraða bílsins á því augnabliki. Meðalgildissetningin segir að á einhverju augnabliki hafi hraði bílsins verið jafn meðalhraðanum, eða að til sé snertill við ferilinn sem er samsíða bláu línunni, og græni snertillinn á myndinni er það einmitt. Tengt efni á Vísindavefnum:
- Hvað eru heildun og deildun og hvernig nýtast þær í leik og starfi? eftir Kristínu Bjarnadóttur.
- Hver er munurinn á falli og vörpun í stærðfræði? eftir Benedikt Steinar Magnússon.
- Hvað er ítrun Newtons? eftir Hildi Guðmundsdóttur.
- Hvaða ástæða er fyrir því að fallið e í veldinu (-x^2/2) er óheildanlegt fall? eftir Stefán Inga Valdimarsson.
- Eggert Briem og Jón Ingólfur Magnússon. Raunfallagreining: Föll af einni raunbreytu. 2001, Háskólaútgáfan.
- Michel Rolle á Wikipedia, frjálsa alfræðiritinu
- Gröf: Vignir Már Lýðsson